동적 프로그래밍(Dynamic Programming)
동적계획법(다이나믹 프로그래밍) 이란, 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다.
이것은 부분 문제 반복과 최적 부분 구조를 가지고 있는 알고리즘을 일반적인 방법에 비해 더욱 적은 시간을 내어 풀 때 사용한다. 라는 의미가 있다. - 위키백과
즉 코딩테스트에서는 DP는 메모리를 사용해서 중복 연산을 줄이고 중복 연산을 줄여서 수행 속도를 개선하는 것
그리고 이미 계산한 결과를 메모리에 저장하여, 다시 계산하지 않도록 하는 것을 목적으로 한다.
DP 알고리즘은 기억하기라고 생각을 하면 좀 더 쉽게 이해가 간다.
Dynamic Programming 조건
동적 프로그래밍은 "큰 문제"를 "부분 문제"로 나누고, "부분 문제"의 정답으로 "큰 문제"의 답을 찾는 알고리즘 설계 기법이다.
동적 프로그래밍의 대표적인 예로 피보나치 수열을 예로 들 수 있다.
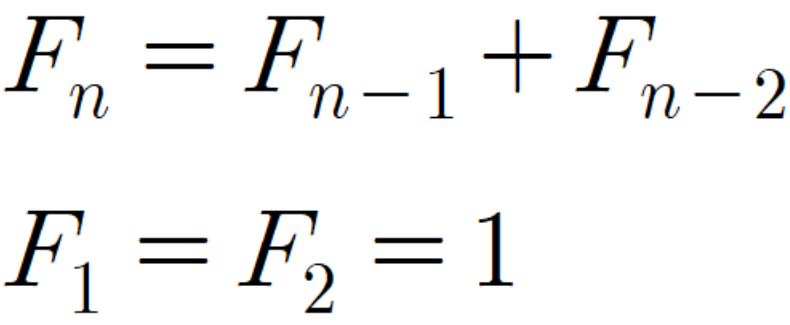
F[1] = 1
F[2] = 1
F[1] = F[2]
F[i] = F[i-1] + F[i-2]
점화식은 재귀식이라고도 하며 위 코드를 보면 피보나치 수열은 재귀적인 관계를 가지고 있다는 것을 알 수 있다.
부분 반복 문제 (Overlapping Subproblem)
피보나치 수열이 해를 찾는 과정을 보면 "큰 문제"를 찾기 위해 "부분 문제"가 필요하고 "부분 문제"는 중복이 된다.
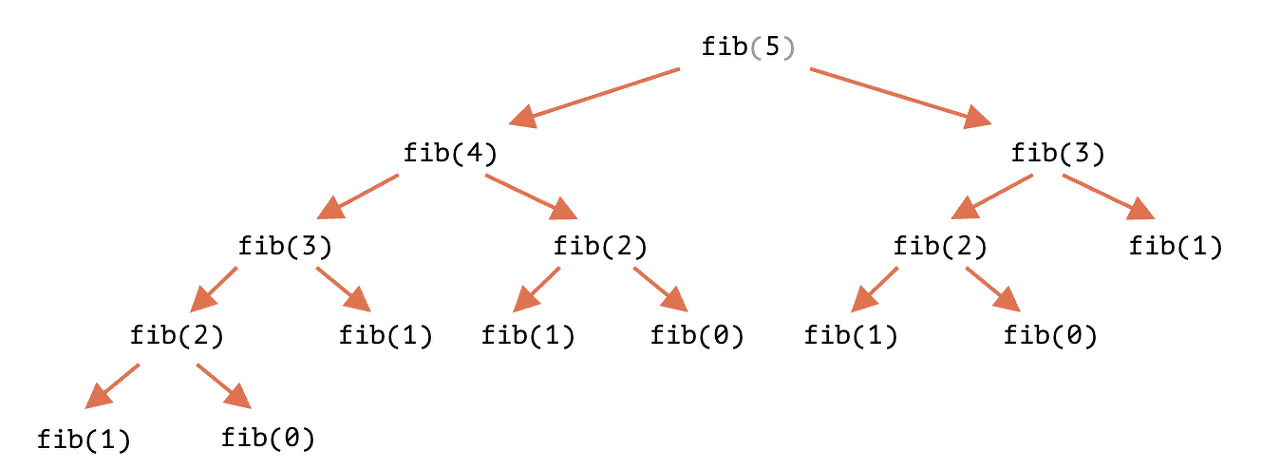
만약 위 점화식을 이용해 fib[4]를 찾기 위해선 "부분 문제" fib[3]과 fib[2]를 찾아야하고, fib[3]은 또 쪼개져 fib[2]와 fib[1]의 해를 찾아야 한다.
fib[4] = fib[3] + fib[2]
fib[4] = (fib[2] + fib[1]) + fib[2]이런식으로 fib[2] 의 해를 이미 했던 연산임에도 한번 더 총 2번을 구해야하는 "중복"이 나타나는데
이러한 반복적인 연산을 부분 반목 문제(Overlapping Subproblem) 라고 한다.
이때, 부분 문제는 항상 새로운 부분 문제를 생성해내기 보다는 계속해서 같은 부분 문제가 여러번 재사용되거나 재귀 알고리즘을 통해 해결되는 문제를 가리킨다.
- 문제 : fib(4)의 해 구하기
- 부분문제 : fib(4-1)의 해 구하기 + fib(4-2)의 해 구하기
최적 부분 구조(Optimal Substructure)
문제"의 조합으로 찾을 수 있으며 문제의 해는 동일한 연산으로 수행되어야 한다.
fib(n) = fib(n-1) + fib(n-2);위 피보나치 점화식에서 큰 문제의 답인 fib(n)이 최적의 답이 되기 위해선, 작은 부분 문제인 fib(n-1)과 fib(n-2)가 최적의 답이 되어야 함
최적 부분 구조를 만족한다면, 문제의 크기에 상관없이 어떤 한 문제의 답은 일정한데 이를 피보나치 수열 그림을 참고해 간단히 설명하면,
fib(5) 에서 구한 fib(3)
fib(4) 에서 구한 fib(3)
fib(3) 에서 구한 fib(3)
이 fib(3) 의 값들이 항상 같은 값인 것이다.
하지만, fib(3) 은 같은 값이기 때문에 여러 번 반복되어 연산하는 것은 비효율적이다. 그렇기 때문에 메모이제이션(Memoization) 이라는 개념이 도입되게 된다.
메모이제이션(Memoization)
동일한 문제를 반복해야 할 경우, 한 번 계산된 결과를 저장해 두었다가 활용하는 방식으로 중복 계산을 줄이는 것
메모이제이션을 통해, 이전에 계산한 값을 메모리에 저장함으로 써, 동일한 계산의 반복 수행이 제거 되어 프로그래밍 실행 속도를 빠르게 할 수 있다.
메모이제이션을 통해 위 피보나치 수열에서 fib(5)를 구할 시 중복되는 연산을 다음 메모이제이션을 통해 해결할 수 있다.
=> 저장해 두는 메모리(배열)을 캐시(Cache)라고 부르기도 한다.
Dynamic Programming 접근방식
Bottom - up 방법
아래서 위로 접근하는 방법으로 부분 문제에서부터 문제를 해결하여 점차 큰 문제를 풀어가는 방식이다. for 문을 이용하는 방식이 이에 해당한다.
public class FibonacciBottomUp {
public static int fibonacci(int n) {
if (n <= 1) {
return n;
}
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
public static void main(String[] args) {
int n = 10; // 원하는 피보나치 수열의 인덱스
System.out.println(fibonacci(n)); // 출력: 55
}
}
Top - Down 방법
위에서 아래로 접근하는 방법으로, 큰 문제에서 부분 문제로 쪼개가면서 재귀 호출을 통해 문제를 푸는 방법이다.
public class FibonacciTopDown {
private static int[] memo;
public static int fibonacci(int n) {
if (n <= 1) {
return n;
}
if (memo[n] == 0) {
memo[n] = fibonacci(n - 1) + fibonacci(n - 2);
}
return memo[n];
}
public static void main(String[] args) {
int n = 10; // 원하는 피보나치 수열의 인덱스
memo = new int[n + 1];
System.out.println(fibonacci(n)); // 출력: 55
}
}
'CS > DataStructure&Algorithms' 카테고리의 다른 글
| [Algorithms & Data structure] ArrayList VS LinkedList (1) | 2024.06.20 |
|---|---|
| [Algorithms & Data structure] Binary Search VS HashMap (0) | 2024.06.17 |
| [Algorithms & Data structure] 탐욕(Greedy) 알고리즘 (1) | 2024.06.10 |
| [Algorithms & Data structure] 시간복잡도 (2) | 2024.06.10 |
| [Algorithms & Data structure] DFS & BFS (0) | 2024.06.10 |
