DFS
루트노트에서 다음 분기로 넘어가기 전, 해당 분기를 모두 탐색하는 방법, 탐색 후에는 다시 원점으로 돌아가 다른 분기를 탐색
특징
- 자기 자신을 호출하느 순환 알고리즘 형태를 지님. (재귀, 스택)
- 이 알고리즘을 구현할 때 가장 큰 차이점은 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사(검사를 하지 않을 경우 무한루프...)
- ex)visit[index] = true;
- 미로를 탐색할 때, 해당 분기에서 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길(새로운 분기)로 돌아와서 다른 방향을 다시 탐색을 진행하는 방법가 유사
- 모든 노드를 방문하고자 할 때, 이 방법을 선택
- 너비우선탐색(BFS)보다 더 간단
- 검색 속도 자체는 너비우선탐색(BFS)에 비해서 느림
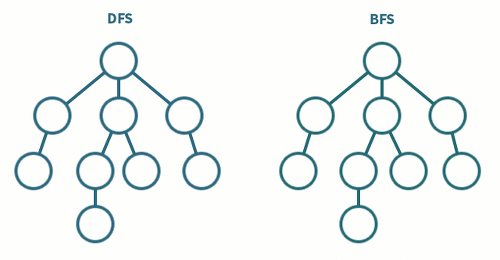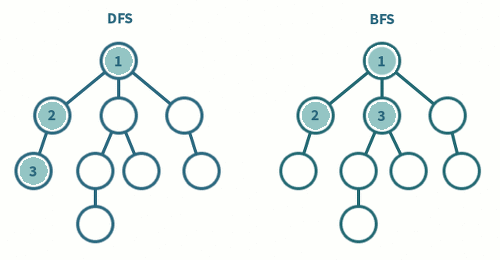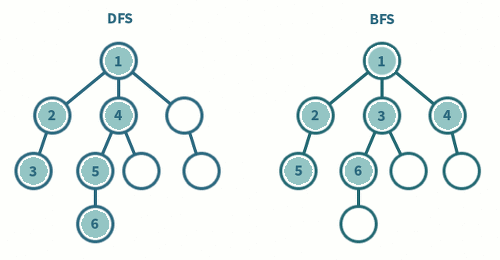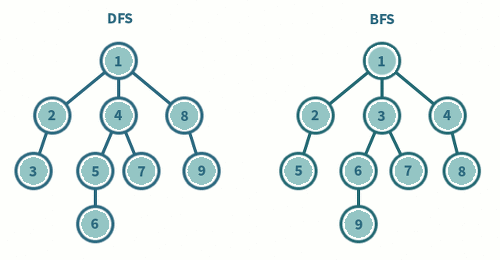
과정
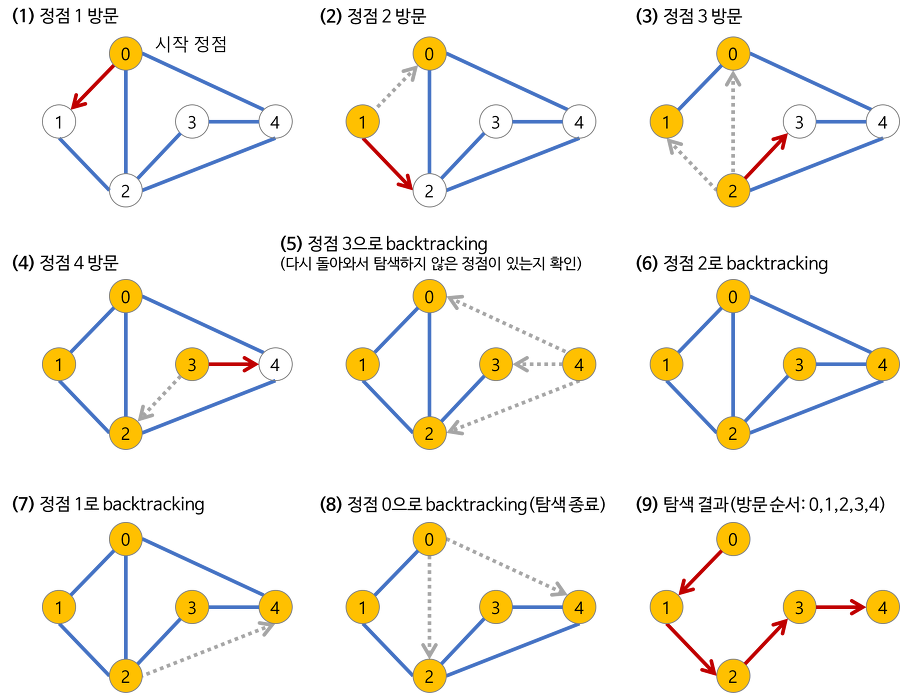
코드
public static void dfs(int start) {
visit[start] = true;
sb.append(start + " ");
for (int i = 1; i <= node; i++) {
if (arr[start][i] == 1 && visit[i] == false) {
dfs(i);
}
}
}
BFS
루드 노트에서 시작한 인접 노드를 먼저 탐색하는 방법
특징
- 재귀적으로 동작하지 않음
- 이 알고리즘 또한, 구현할 때 가장 큰 차이점은 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야한다는 점(이또한 하지 않으면 무한루프.........)
- BFS는 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 자료 구조인 큐를 사용
- 즉, 선입선출 원칙으로 탐색
- 시장 정점으로부터 가까운 정점을 머저 방문하고 멀리 떨어져 있는 정점을 나주에 방문하는 순회 방법
- 깊게(deep)탐색하기 전에 널게(wide) 탐색
- 두 노드 사이의 최단 경로 혹은 임의의 경로르 찾고 싶을때 이 방법을 사용
- ex) 지구 상 존재하는 모든 친구 관계를 그래프토 표현한 후 A 와 B 사이에 존재하는 경로를 찾는 경우
- DFS : 모든 친구 관계를 다 살펴본다
- BFS : A와 가까운 관계부터 탐색
과정
깊이가 1인 모든 노드를 방문하고 나서 그 다음에, 깊이가 2인 모든 노드를, 그 다음엔 깊이가 3인 모든 노드를 방문하는 식으로 계속 방문하다가 더 이상 방문할 곳이 없으면 탐색을 마침
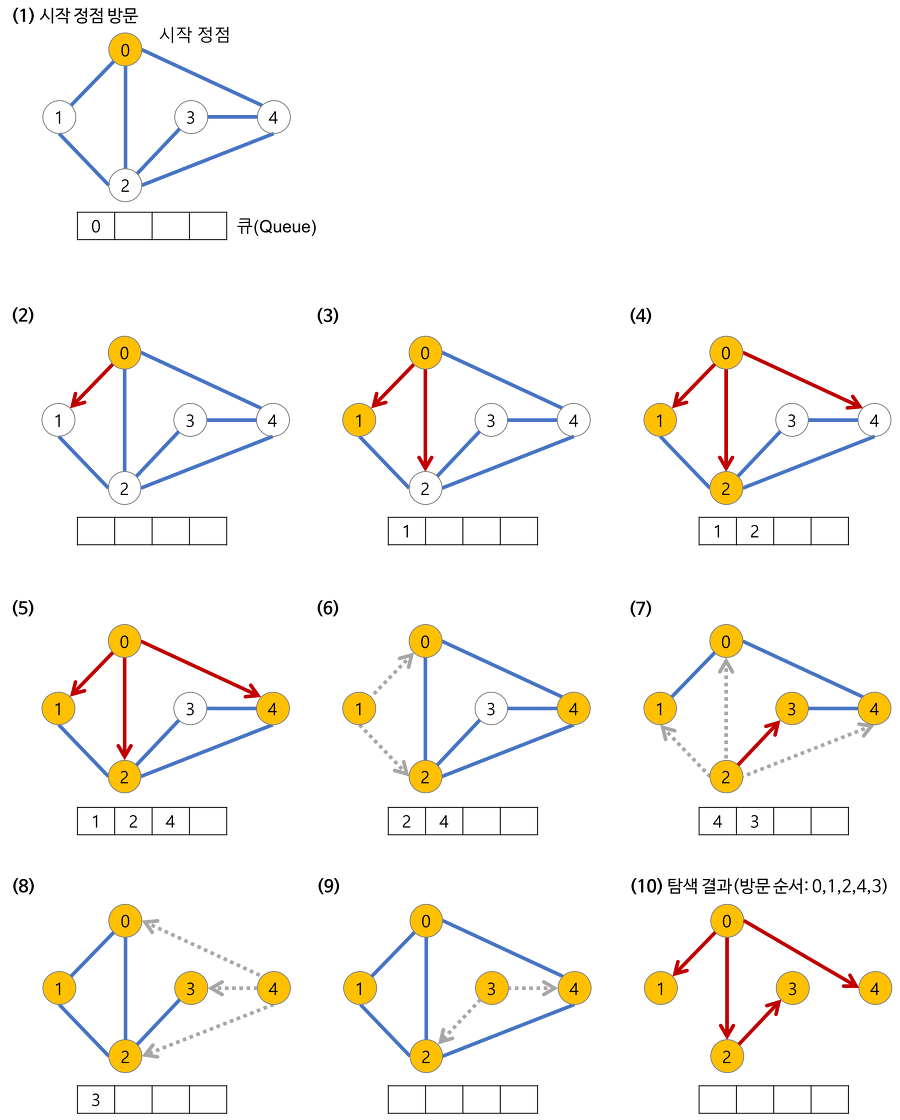
코드
public static void bfs(int start) {
que.offer(start);
visit[start] = true;
while(!que.isEmpty()) {
int temp = que.poll();
sb.append(temp + " ");
for(int i = 1; i < node+1; i++) {
if(arr[temp][i] == 1 && visit[i]==false) {
que.offer(i);
visit[i] = true;
}
}
}
}
BFS와 DFS의 차이
- DFS은 깊게 BFS은 넓게 탐색
'CS > DataStructure&Algorithms' 카테고리의 다른 글
| [Algorithms & Data structure] Binary Search VS HashMap (0) | 2024.06.17 |
|---|---|
| [Algorithms & Data structure] Dynamic Programming (2) | 2024.06.10 |
| [Algorithms & Data structure] 탐욕(Greedy) 알고리즘 (1) | 2024.06.10 |
| [Algorithms & Data structure] 시간복잡도 (2) | 2024.06.10 |
| [Algorithms & Data structure] 스택 & 큐 & 이진탐색 (1) | 2024.06.10 |

